오일러 투어 테크닉(euler tour technique)
오일러 투어 테크닉이란 DFS로 트리를 탐색하면서 임의 정점 \(v\)의 진입 시점과 탈출 시점을 기록하여 트리의 서브 트리를 일차원 배열로 관리하는 테크닉이다.
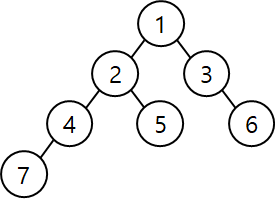
과정
1. 루트부터 DFS를 시작해 각 정점의 진입 순서를 left 배열에 기록하자. (0-base, 1-base 상관없다.)

2. 탈출 순서를 right 배열에 기록하자

3. 트리와 left, right 배열을 한 번에 보면, 정점 v를 루트로 하는 서브 트리에 속한 정점들의 방문, 탈출 순서가 모두 루트 정점에 진입, 탈출 순서 사이에 있다. 즉, 각 정점을 루트로 하는 서브 트리가 하나의 구간으로 나타난다.

구현 방법
진입 순서와 탈출 순서를 어떻게 관리할까? 전역 변수를 이용하여 관리할 수 있다. order 전역 변수를 이용해보자.
DFS에 진입했을 때 배열 left에 order 값을 저장하여 진입 순서를 저장하고 인접한 정점을 탐색하면서 order 값을 업데이트 한 다음, DFS가 종료될 때 정점에서 나오는 것이므로 right 배열에 order 값을 저장하면 된다.
int order = 0;
void dfs(int here){
l[here] = ++order;
for(const int& there: adj[here]){
dfs(there);
}
r[here] = order;
}서브트리 관련 쿼리 처리
오일러 투어를 사용하면 트리를 일차원 배열로 변환하여 서브트리 구간을 단일 구간으로 표현할 수 있다. 때문에 트리에서 다양한 구간 쿼리 문제를 트리 기반 자료구조에서 구간 기반 자료구조로 변환하여 더 쉽게 해결할 수 있다.
관련 문제
[P2] 트리와 색깔
머지 소트 트리에서 사용하는 문제
[P3] 주식회사 승범이네
세그 먼트 트리에서 사용하는 문제