스패닝 트리
스패닝 트리란 무향 그래프의 모든 정점을 연결하는 부분 그래프이다. 간선의 개수는 \(V-1\) 개로 트리 구조이다. 그림 1은 7개의 정점을 6개의 간선을 이용해 연결하는 올바른 스패닝 트리이다. 반면에 그림 2는 0-1-2의 정점으로 이루어진 사이클이 있으며 2, 4번 정점은 연결되어 있지 않으므로 스패닝 트리가 아니다.
 |
 |
| 그림 1 | 그림 2 |
최소 스패닝 트리
최소 스패닝 트리란 가중치가 있는 무향 그래프의 스패닝 트리 중에서 가중치의 합이 최소인 스패닝 트리이다. 최소 스패닝 트리를 구하는 알고리즘은 크루스칼 알고리즘과 프림 알고리즘이 대표적이다.

크루스칼 알고리즘
가중치가 큰 간선과 가중치가 작은 간선 중 어떤 간선이 최소 스패닝 트리에 포함될 가능성이 높을까? 당연히 가중치가 작은 간선이 최소 스패닝 트리에 포함될 가능성이 높을 것이라고 생각할 수 있다. 그렇다면 모든 간선을 가중치가 작은 순서로 순회하여 해당 간선을 추가해도 여전히 트리 구조를 만족하면 스패닝 트리에 추가해보자.
가중치가 제일 작은 0-1 간선을 추가해도 트리 구조를 만족하므로 추가하자.

0-2 간선을 추가해도 트리 구조를 만족하므로 추가하자.

1-2 간선을 추가하면 사이클이 생기므로 추가하면 안 된다.
 |
 |
2-4 간선을 추가해도 트리 구조를 만족하므로 추가하자.

0-3 간선을 추가해도 트리 구조를 만족하므로 추가하자.

1- 4 간선을 추가하면 사이클이 생기므로 추가하면 안 된다.
 |
 |
3-4 간선을 추가하면 사이클이 생기므로 추가하면 안 된다.
 |
 |
3-5 간선을 추가해도 트리 구조를 만족하므로 추가하자.
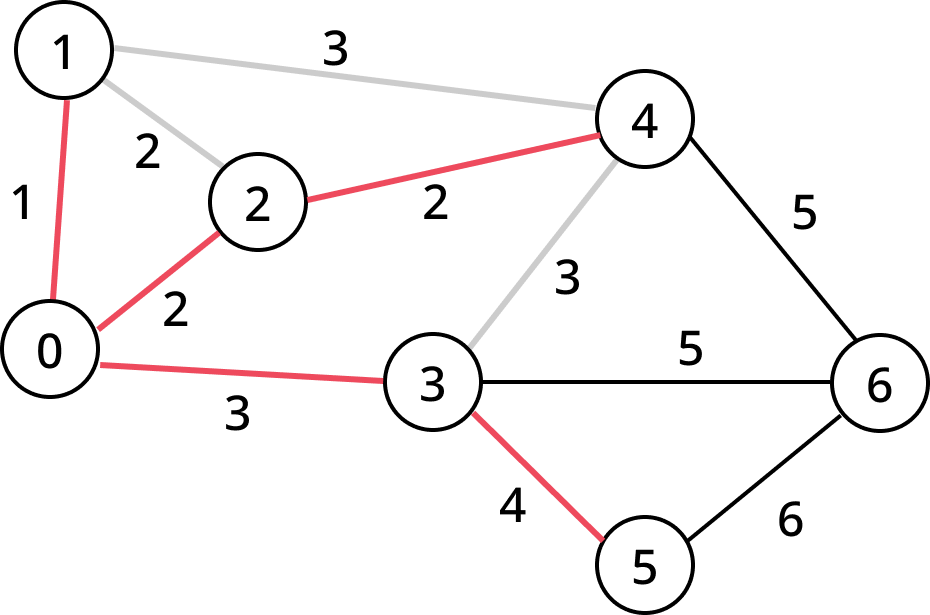
3-6 간선을 추가해도 트리 구조를 만족하므로 추가하자.

4-6 간선을 추가하면 사이클이 생기므로 추가하면 안 된다.
 |
 |
마지막으로 5-6 간선을 추가하면 사이클이 생기므로 추가하면 안 된다. 모든 간선을 순회했으므로 최소 스패닝 트리가 완성됐다.
 |
 |
크루스칼 알고리즘 동작 과정
- 간선의 목록을 가중치 순서대로 오름차순 정렬한다.
- 모든 간선을 순회하며 이미 선택한 간선과 사이클이 생기지 않으면 스패닝 트리에 추가한다.
2번 과정을 어떻게 할 수 있을까? BFS 또는 DFS를 사용해 트리를 탐색하여 사이클이 있는지 확인할 수 있다. DFS의 경우 트리의 간선을 추가한 뒤 역방향 간선이 있는지 판별하면 사이클을 판단할 수 있다. 모든 간선마다 탐색을 수행해야 하므로 \(O(E^2)\)이 소요된다. 2번 과정을 더 빠르게 하기 위해서는 유니온 파인드 자료구조를 사용해야 한다.
유니온 파인드는 서로소 집합을 표현하는 자료구조로 합치기(union)과 찾기(find) 연산을 지원한다. 두 정점이 같은 집합에 속하지 않으면 합치기 연산으로 같은 집합으로 만들 수 있다. 만약 추가하려는 간선의 두 정점이 같은 집합에 속한다면 사이클이 있는 것으로 판별할 수 있다. 따라서 유니온 파인드를 사용하여 크루스칼 알고리즘의 시간 복잡도를 \(O(ElogE)\)로 줄일 수 있다.
정당성 증명
매 순간 가중치가 가장 작은 간선을 선택하기 때문에 크루스칼 알고리즘은 그리디 알고리즘으로 볼 수 있다. 크루스칼 알고리즘이 올바르게 동작하는지 증명해보자.
크루스칼 알고리즘이 선택한 간선 \((u, v)\)이 최소 스패닝 트리에 포함되지 않는다고 가정하자. 즉 선택한 간선 \((u, v)\)는 크루스칼 알고리즘이 잘 못 선택된 간선이다.

크루스칼 알고리즘이 간선 \((u, v)\)를 잘못 선택했지만 만약 크루스칼 알고리즘이 올바르게 동작하여 만들어진 진짜 스패닝 트리가 존재한다면 진짜 스패닝 트리에서는 정점 \(u\)와 \(v\)는 다른 정점들로 구성된 다른 경로로 연결되어 있을 것이다. 이때 이 경로의 간선들은 \((u, v)\)의 가중치보다 크거나 같다. 왜냐하면 \((u, v)\) 의 가중치보다 작다면 먼저 크루스칼 알고리즘에 의해 선택되어 연결되었을 것이고 \((u, v)\) 간선을 선택하면 사이클이 형성되기 때문에 크루스칼 알고리즘에 의해 애초에 \((u, v)\) 간선이 선택되지 않았을 것이기 때문이다.

그렇다면 이 경로상에서 간선 \((u, v)\) 가중치 이상의 가중치를 갖는 간선을 하나 골라 끊고 \((u, v)\)를 연결하면 스패닝 트리의 가중치 합이 더 작아진다. 따라서 가정했던 크루스칼 알고리즘이 선택한 간선 \((u, v)\)는 올바른 간선이므로 \((u, v)\)가 잘못된 간선이라는 가정에 모순이다.

따라서 \((u, v)\)를 선택하여도 남은 간선들을 잘 선택하면 항상 최소 스패닝 트리를 완성할 수 있다.